Visualization of Deep Analysis using the Matrix as source videos
About
Deep Analysis is a part of Autonomous Video Artist. An ongoing project that I work for Benjamin Grosser. The question the project tries to answer is what if the process of making videos doesn't involve any human interference. The robot we are using will shoot videos and edit videos not by human aesthetic standards but a chain of evolving computational rules. My role in the project is to write an editing system and a deep analytical tool for our robot to edit videos together. And Deep Analysis is that analytical tool that I wrote during 2017 summer. The Deep Analysis provides rather computationally complicated angles for the robot to view videos it shoots. For us to better view those analysis, I also devised visualizations to translate what robot is "thinking " to a human understandable format. The Deep Analysis involves Gradient Analysis, Feature Analysis and Fourier Transform Analysis with their corresponding visualizations.
Gradient Analysis
Gradient calculation is one of the most used technique in computer vision, especially in edge finding algorithms like Canny, Sobel methods. The Deep Analysis will calculate all the pixel gradients from an image and use them as a guideline for the robot to edit videos. In the calculated result, each pixel contains a gradient vector with direction and intensity. To visualize the gradient analyzing process, each pixel will be recursively connected to its neighboring pixels with same gradient directions. Different gradient directions will have different colors and the intensity of each gradient vector will be normalized to be used directly as pixel intensity in the visualization. Below is a sample image from the move Matrix and its corresponding gradient analysis visualization.
Feature analysis
In the Deep Analysis, all image corners will be extracted as image features. The Deep Analysis will run The Harris & Stephens corner detection algorithm on all the input images. However, instead of outputting all the corner pixels of an image, the Deep Analysis will output a matrix with the same dimension as the input image. In the output matrix, each cell will contain a 2x2 matrix with 2 eigenvectors and eigenvalues. The larger the eigenvalues, the bigger the possibility that their corresponding pixel is a corner. To visualize this analytical process, each of the 2x2 matrix will be represented as a ellipse. The eigenvectors will determine the orientation of the ellipse and the eigenvalues will determine the magnitudes of both major and minor axises. Below is a sample image from the movie Matrix and its corresponding feature analysis visualization
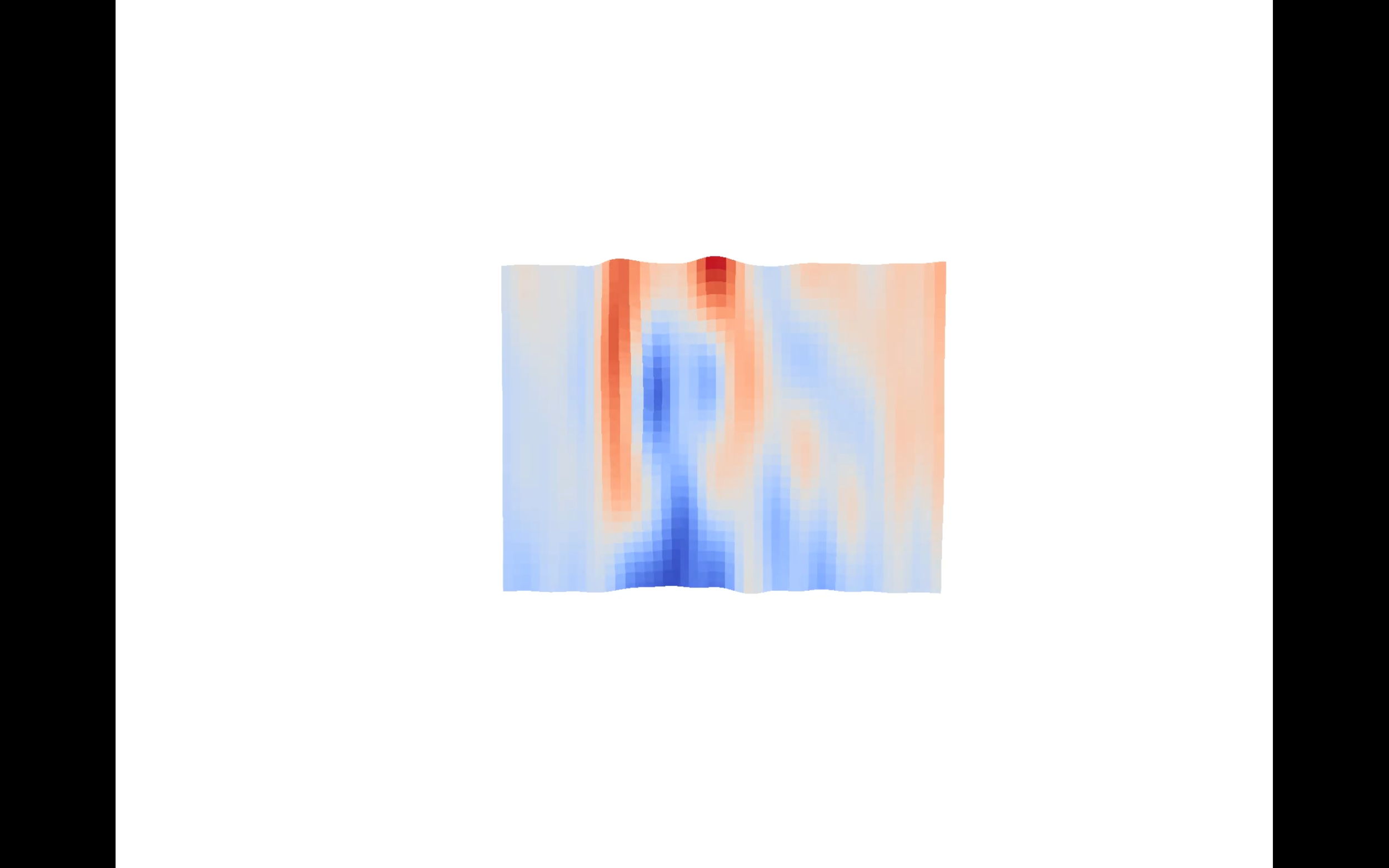
Fourier transform Analysis
1D Fourier Transform decomposes a 1D signal into bunch of 2D sin and cos waves. The same logic can be applied to 2D Fourier Transform as 2D Fourier Transform will decompose a 2D signal into bunch of 3D sin and cos waves (surfaces). The Fourier Transform Analysis will treat each image as a single 2D signal and decompose it into a collection of 3D surfaces and output it to the robot. The visualization compiles all the generated high energy surfaces from one image together into a single 3D surface. The 3D surface will exhibit some original image's features. Below are images of a surface viewed from different angles and its corresponding image from the movie Matrix.
Future work
I will continue working on Autonomous Video Artist. Our plan is to finish the editing system within 2017 so that we can test run the whole project in early 2018 and hopefully finish it before March.